ハッセ図とは？基本知識・書き方を紹介

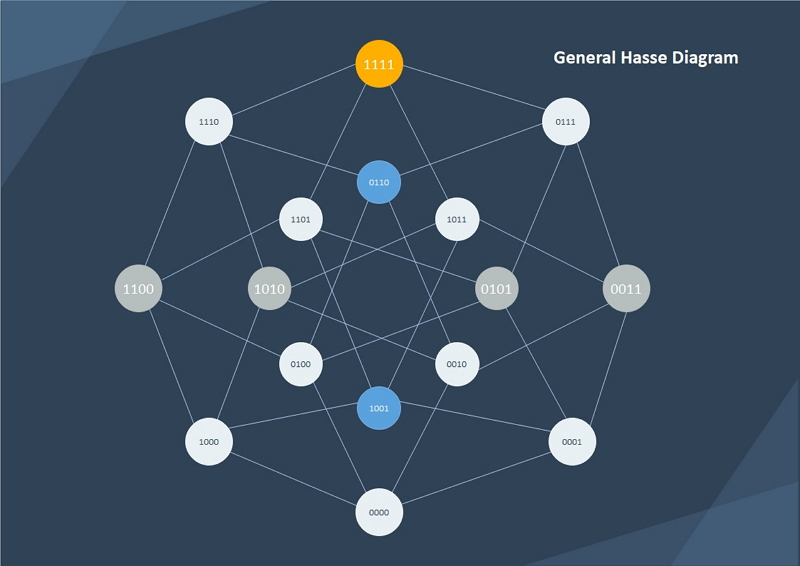
1. ハッセ図について

ハッセ図（hasse diagrams）は、有限な半順序集合（POSET: 部分順序集合）をグラフィカルに表す図で、日本語では「ハッセ図」と呼ばれることが多いです。POSETの要素は●（点）で、要素間の関係は直線で示されます。ハッセ図は、集合やその関連理論の学習、ブール代数の表現などでとても役立つツールです。

元々、ハッセ図の作成は手書きでPOSETを表現していましたが、今ではさまざまなグラフ作成ツールで、より簡単に描けるようになっています。

ここでは、ハッセ図に線分を描く際に押さえておきたいポイントをまとめました：

1. POSET内の要素がもう一方より大きい場合、小さい方が下、大きい方が上になります。例えば x, y という要素で x > y なら、x のほうが上位です。
2. POSET内に x と y、または y と x の関係があれば、2つの要素間に直線を引きます。

1.1 ハッセ図の関係性について

ハッセ図という名称はヘルムート・ハッセに由来します。実際には彼が最初に考案したものではありませんが、POSETを図として表すきっかけを作った人物です。ハッセ図には部分集合をバイナリ（1または0）で表すこともできます。図の形や大きさもさまざまです。

もっともシンプルなハッセ図（一筆書きできる場合）は直線状ですが、複雑になると立体的や4x4マトリクスになることもあります。ハッセ図上の要素同士の関係には次のようなルールがあります：

1. 反射性 → p ≤ p Ɐ p ꞓ B
2. 反対称性 → p ≤ q かつ q ≤ p のとき、p=q
3. 推移性 → p ≤ q, q ≤ r の時、p ≤ r

ハッセ図の場合：

1. POSET内で、他のどの要素よりも小さい要素は「極大元」と呼ばれます。
2. 同時に、「極小元」は他のどの要素よりも大きくない要素を指します。
3. POSET内で他の全てを上回る要素は「最大元」、すべて他に先行する要素は「最小元」と呼ばれ、これらは通常ハッセ図上で一つのみ存在します。
4. ハッセ図の極大元と極小元は同じ場合もあり、どの集合を扱うかによります。

2. ハッセ図の描き方

部分順序集合の順序関係を直感的に理解したい学生さんには、ハッセ図がオススメです。ただし、手書きで完璧なハッセ図を作るのは意外と難しいですよね。

2.1 ハッセ図をゼロから描く手順

ハッセ図を描く基本ステップを以下にまとめました：

ステップ1: ハッセ図は「順序図」とも呼ばれます。まずPOSETの部分順序を有向グラフで描き出します。

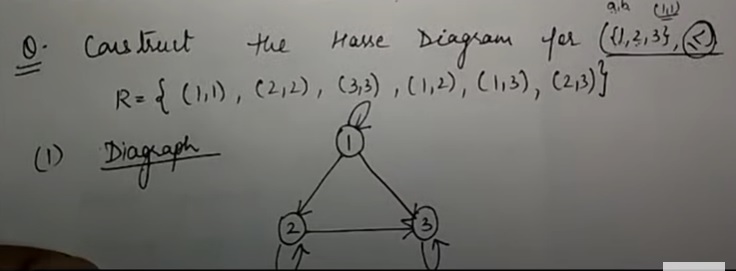
ステップ2: 次に、各頂点についた自己ループを消去し、推移性によって成り立つ関係（直接線を引かなくていいもの）は省略します。例えば1R2、2R3、1R3の3つの要素がある場合、1R3は推移性で成り立つので消去します。

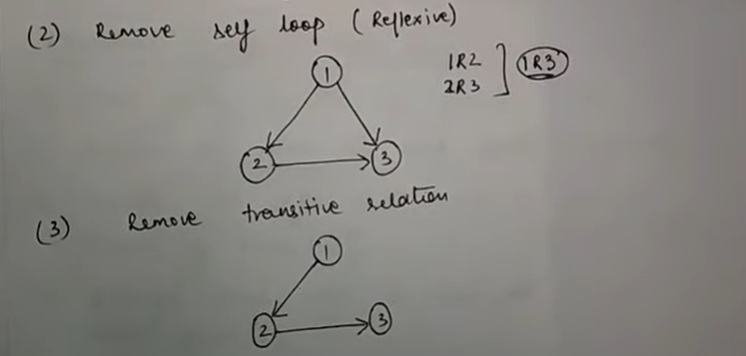
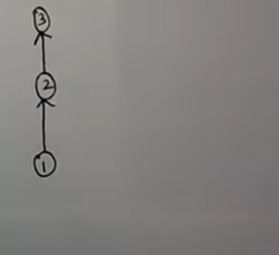
ステップ3: 続いて、エッジ（線）が上向きになるように配置し、最後に矢印を消して、各ノードは●（点）で表現します。これでハッセ図らしい形に！

2.2 オンラインでハッセ図を作成する方法

「本当にこれで合ってる？」と迷うこともあるかもしれません。ハッセ図は反射性・推移性などの性質を注意しないと、ミスしがち。そんな時はEdrwaMaxの使用がイチ押しです！初心者でも直感的に操作できるので、図解経験ゼロでも大丈夫。シンプルなUIで大人気です。

たとえば EdrawMaxなら280種類以上の図がオンラインで作れるから、利用者は全世界で2500万人突破とか。手書きじゃなくEdrawMaxでハッセ図をサクッと作成できます。作り方はとっても簡単：

ステップ1:まずはEdrawMaxを開き、「科学」タグを見つけてクリックします。ハッセ図を探すには、「数学」タブからハッセ図を選びます。ツール内には理科・教育に関する多彩なテンプレ・動画も揃っていて、授業でも活用できます。UIは日本語対応でとても使いやすいですよ。

ステップ2: 

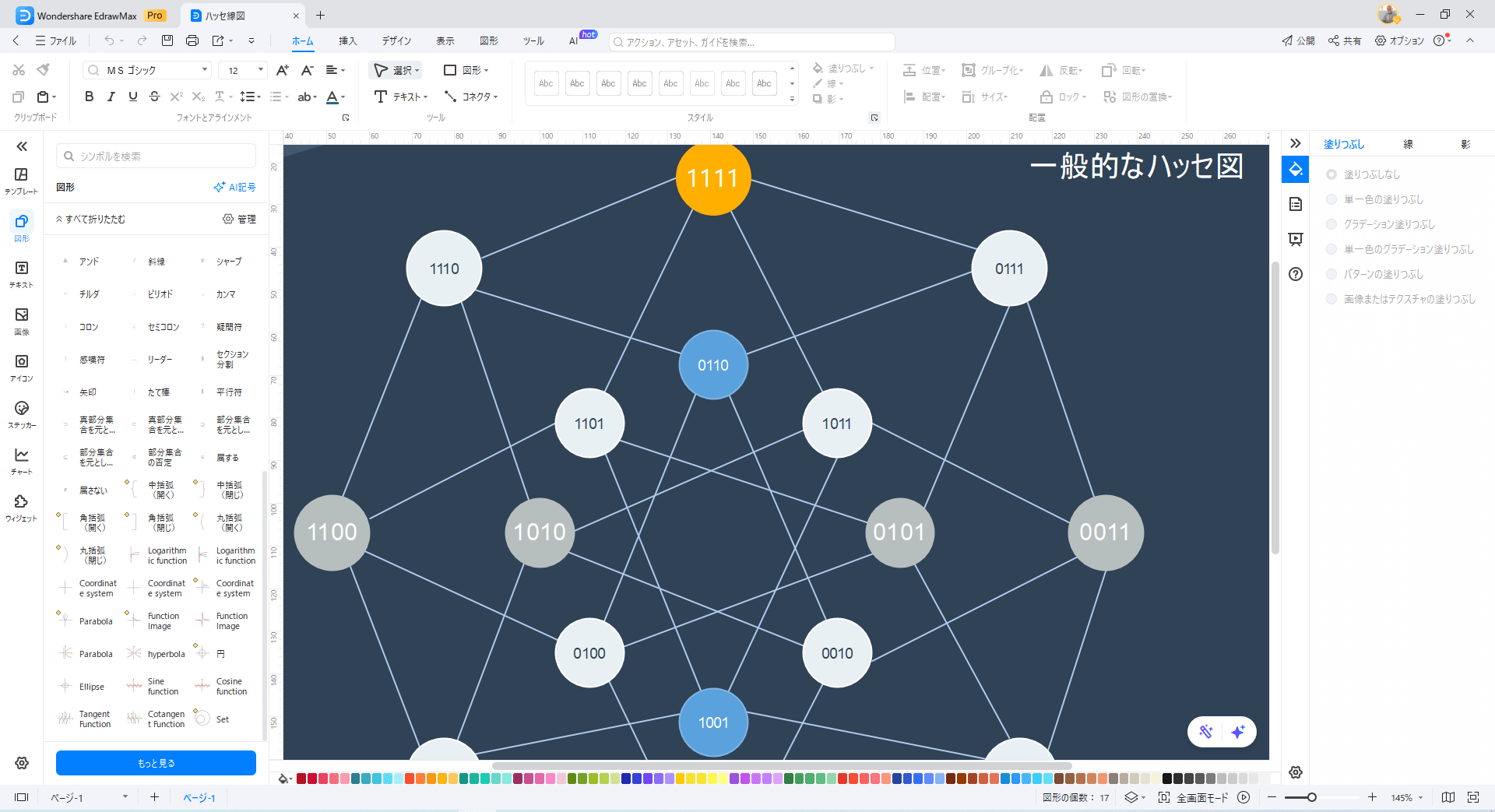
テンプレを選んだ後は、自分の学習内容にあわせて図を編集すればOK！高品質なテンプレートが多いので、軽いアレンジだけで仕上げられます。

ステップ3:  編集が終わったら、保存・エクスポートしておけば今後も使えます。複数の形式で保存でき、授業・レポート・論文でも再利用可能！また EdrawMaxは様々なデバイス・OSに対応、いつでもどこでもハッセ図編集できちゃいます。

3. ハッセ図の例

このハッセ図は、部分順序集合をわかりやすく可視化する方法です。いくつか具体例を紹介します：

集合A={5,6,7,8}とし、A上の「≤」という関係Rについてハッセ図を描きます。

R={{5,5}, {5,6}, {5,7}, {5,8}, {6,6}, {6,7}, {6,8}, {7,7}, {7,8}, {8,8}}

反射性で削除: (5,5), (6,6), (7,7), (8,8)

推移性で削除: (5,7), (5,8), (6,8)

2つめの例は、集合（4,6,24,32,48,72）の倍数関係をハッセ図にする問題です。集合Aであれば：

A = {{4,24}, {4,32}, {4,48}, {4,72}, {6,24}, {6,48}, {6,72}, {24,48}, {24,72}}

18の正の約数

集合D={1,2,3,6,9,18} のとき、POSET A={{1,2},{1,3},{1,6},{1,9},{1,12},{1,18},{2,6},{2,18},{3,6},{3,9},{3,18},{6,18},{9,18}}

4. まとめ

集合論や部分順序集合の理解には、ハッセ図を利用することが近道です。ハッセ図手書きだとハッセ図作成は一苦労で、時間もかかります。理想的なハッセ図を作れないことも…。そんな時は使いやすいEdrawMaxがオススメ。誰でもキレイなハッセ図が手軽に作れます！